Basic Formulas
Focal Length of Eyepieces
The magnification of the telescope is given by the focal length f of the
eyepiece. Magnification V is simply (with F as focal length of the telescope):
![]() (1)
(1)
therefore e.g. for f=4mm, F=1000mm a magnification of 250.
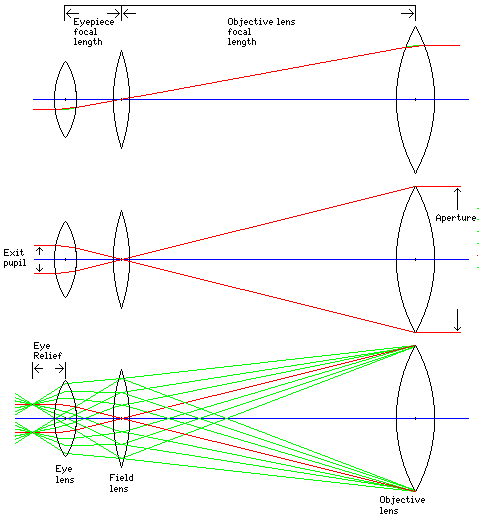
Figure 1: Graphic for some
important definitions
Which magnifications are useful?
The smallest useful magnification is given, if the exit pupil is as big
as the eye’s pupil, if adapted to darkness. This is about 7 to 8mm, depending
on the observers age. If a smaller magnification is chosen, the exit pupil will
increase and the amount of light outside the eye’s pupil will be lost.
Therefore it is possible to use these smaller magnifications, but the image
will be identical to that of a smaller telescope – according to the light lost.
The exit pupil A is calculated by the aperture ration of the telescope
(lens resp. mirror diameter D divided by the focal length F) and the focal
length of the eyepiece. The formula is given by:
![]() (2)
(2)
For the smallest magnification one will get:
![]() (3)
(3)
The lowest useful magnification is therefore dependent only on the lens resp.
mirror diameter! The according maximum focal length of the eyepiece is:
![]() (4)
(4)
That is for a system with an aperture ratio of F/D=6 an eyepiece with
48mm focal length.
For the useful maximum magnification I would like to make a short
excursion.
The maximum theoretical resolution of a telescope is limited by
diffraction at the edge of the objective (lens or primary mirror). Without any
derivation the common value in use for this resolution is given by
![]() (5)
(5)
That means, that an instrument with an objective diameter of 140mm is
able to resolve two lines if their distance is bigger than 1“ (1 arc second).
280mm will lead to a resolving power of 0.5”, 70mm to 2”.
At the end of the telescope another optical element is placed – the
human eye. The human eye, caused by the distance of light sensitive cells in
the retina, is able to resolve an angular distance of about 1 arc minute. From
this it follows that the maximum magnification VRes, at which in
principle the maximum resolving power of the telescope is used, is given by
![]() (6)
(6)
That is for an objective of 200mm diameter just a magnification of 86!
Any magnification which is going ahead this limit will lead to a “diffuse”
image! But there are a couple of reasons to use much higher magnifications:
- At low
illumination levels, and this is the case in most of astronomical
observations, the eye’s resolution is going down to 2 or 3 arc minutes.
According to this the magnification can be increased unless the impression
of an diffuse image occurs.
- It is very
exhausting to view details at the edge of the eye’s resolution power.
Magnification beyond the theoretical limit leads to more relaxed viewing.
- Planets are
very bright at low magnifications. Using higher magnification reduces the
area brightness and contrasts become more obvious.
For this the practical limit for the maximum magnification is not given
by D [mm]* 0,43, but
![]() (7)
(7)
For refracting telescopes you will find up to D [mm] * 2,5.
The according minimum focal length of the eyepiece is given by
![]() (8)
(8)
This is e.g. for a system with focal length F=1000mm and objective
diameter of 100mm an eyepiece focal length of 5mm.
Field of
View
You have to differentiate between “apparent field of view (AV)“ and
“real field of view (RV)“.
The apparent field of view is characteristic for an eyepiece and does
not depend on the telescope used. It is the viewing angle when looking into the
eyepiece. Depending on the eyepiece design apparent field of views differ from
about 30° (Huygens) to about 82° (Nagler type). To give a vivid example, if
looking into a Huygens eyepiece you will have the impression of looking into a
tunnel, whereas the view into a wide angle eyepiece will you make feel as if
sitting in the first row of a cinema.
The real field of view is the area on the sky, given in degrees, which
you will see if looking through the telescope. It is dependent on the apparent
field of view, but also on the magnification as defined above. The formula is
![]() (9)
(9)
From this it is clear that for the same magnification you will see with
a wide angle eyepiece (70° AV) an area with a diameter 2.3 time bigger than
with an orthoscopic eyepiece (30° AV), if both eyepieces have the same focal
length. I.e. the area visible with the wide angle is increased by a factor of
5.4! For the observation of large objects wide angle eyepieces are therefore
recommended, the impression when viewing through the telescope is really
impressive.
Real field of views are varying from about 3° (31mm Nagler type with
telescope of focal length 800mm) down to a few arc minutes.
Comment for advanced readers:
Formula (9) is commonly used
(so by us), but however it is not correct at all. The formula neglects any
distortion effects, and distortion lead to the fact that magnification is not a
constant over the complete field of view. In case of pincushion distortion the
magnification increases towards the edge of the field of view. As we use
formula (9) for our measurements of the apparent field of view, our results for
the AV are somewhat less (about 0° to 3°, depending on the distortion level) than
the “real” AV according to its definition. The advantage is, that if you use our
AV measurement results and calculate your RV by formula (9), you will get a
correct result. The disadvantage is, that there are inherently differences
between the manufacturers AFoV and ours.
The maximum apparent field of view is limited by physics for a given
diameter of the field lens. It can be calculated from the focal length of the
eyepiece and the diameter of the field lens resp. field stop:
 (10)
(10)
For attention: If yoou use
your pocket calculator in setting „rad“, or if you use Excel for the
calculation, you have to multiply with a factor 180/π (arctan in radian!).
The field lens diameter is clearly limited by the eyepieces insertion
diameter. Eyepieces are available with diameters of 24.5mm, 1 ¼” and 2”. Depending
on the focal length of the eyepiece the maximum possible apparent field of view
is given in the following table. The values are theoretical, as the sleeve has
an inner diameter which is less than the insertion diameter. Therefore the
reachable field of view is some degrees less than given here.
|
Insertion Diameter |
Focal Length of Eyepiece (mm) |
Maximum Apparent Field of View (°) |
|
24.5mm |
15 |
78,5 |
|
|
20 |
63,0 |
|
|
25 |
52,2 |
|
|
30 |
44,4 |
|
|
40 |
34,1 |
|
31,8mm (1 ¼“) |
15 |
93,3 |
|
|
20 |
77,0 |
|
|
25 |
64,9 |
|
|
30 |
55,8 |
|
|
40 |
43,4 |
|
50,8mm (2“) |
25 |
90,9 |
|
|
30 |
80,5 |
|
|
40 |
64,8 |
|
|
50 |
53,9 |
|
|
80 |
35,2 |
Table 1: Maximum Apparent
Field of View for Eyepieces with different Insertion Diameters and Focal
Lengths.
Bigger apparent field of views are not possible without distortion! From
this table it becomes clear where to use the big 2“-eyepieces: at long focal
lengths, if the required apparent field of view is not reachable with smaller
eyepieces. However, at e.g. 15mm focal length one can achieve exactly the same
apparent field of view either with a 1 ¼“ eyepiece than with an 2“ eyepiece.