Kennzahlen
Okularbrennweite
Die Kennzahl für die am
Teleskop erreichte Vergrößerung ist die Okularbrennweite f. Die Vergrößerung V
ist einfach (mit F als Teleskopbrennweite):
![]() (1)
(1)
Also z.B. für f=4mm,
F=1000mm eine 250-fache Vergrößerung.
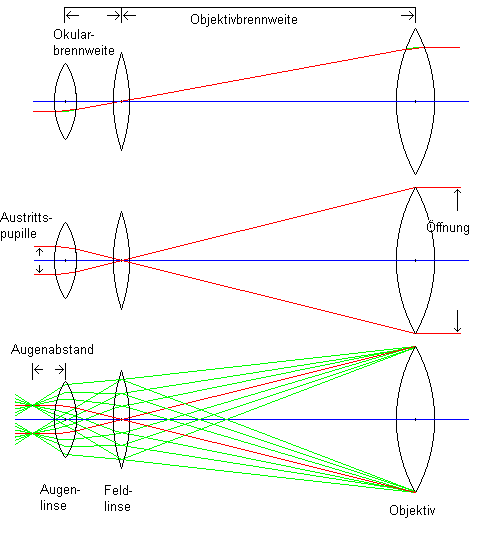
Abbildung 1:
Einige wichtige Begriffe in anschaulicher Grafik
Welche Vergrößerungen sind
sinnvoll?
Die kleinste Vergrößerung
ergibt sich dann, wenn die Austrittspupille am Okular so groß ist wie die
Eintrittspupille des auf dunkel adaptierten Auges, also 7 bis 8mm. Bei
kleineren Vergrößerungen und damit größeren Austrittspupillen gelangt nicht
mehr alles Licht in das Auge. Sie sind zwar möglich, das Bild ist jedoch
identisch mit dem eines Instrumentes kleineren Linsen- bzw. Spiegeldurchmessers
- entsprechend des Lichtverlustes.
Die Austrittspupille A
berechnet sich einfach aus dem Öffnungsverhältnis des Teleskopes (Linsen- bzw.
Spiegeldurchmesser D zu Brennweite F) und der Okularbrennweite f. Der Zusammenhang
ist:
![]() (2)
(2)
Für die Minimalvergrößerung
ergibt sich also
![]() (3)
(3)
Die untere Grenze der
Vergrößerung hängt also nur vom Linsen- bzw. Spiegeldurchmesser ab! Die
entsprechende längste Okularbrennweite ist
![]() (4)
(4)
also für ein System mit
einem Öffnungsverhältnis von 1/6 maximal 48mm.
Für die sinnvolle
Maximalvergrößerung möchte ich ein wenig ausholen.
Die maximale theoretische Auflösung
eines Teleskopes ist durch die Beugung am Rand des Objektives begrenzt. Ohne
Herleitung sei hier der Standardwert für diese theoretische Grenze genannt:
![]() (5)
(5)
D.h. also, dass ein
Instrument mit Objektivdurchmesser 140mm ein Auflösungsvermögen von 1“ (eine
Bogensekunde) hat, bei doppeltem Durchmesser 0,5“, bei 70mm 2“.
Hinter dem Teleskop sitzt
als weiteres optisches Element das Auge. Dieses ist, aufgrund des Abstandes der
lichtempfindlichen Zellen auf der Netzhaut, in der Lage ca. 60“ oder eine
Bogenminute aufzulösen. Die Vergrößerung VAuflösung, bei der man
prinzipiell das Auflösungsvermögen des Instrumentes bereits voll ausnutzt, ist
daher
![]() (6)
(6)
Also bei einem 200mm
Objektiv gerade einmal 86-fach. Jede weitere Vergrößerung führt zu einem
„unscharfen“ Bild. Aus verschiedenen Gründen ist es dennoch sinnvoll, höhere
Vergrößerungen einzusetzen:
- Bei geringer Beleuchtung, also z.B. bei Deep-Sky
Beobachtungen, sinkt das Auflösungsvermögen des Auges auf ca. 2 bis 3
Bogenminuten. Dementsprechend kann auch stärker vergrößert werden, bis ein
unscharfer Eindruck entsteht.
- Es ist sehr anstrengend, Details an der Grenze
des Auflösungsvermögens des Auges erkennen zu wollen. Eine höhere
Vergrößerung ermöglicht entspannteres Sehen.
- Planeten sind bei kleineren Vergrößerungen sehr
hell. Durch höhere Vergrößerung wird die Flächenhelligkeit reduziert,
Kontraste kommen besser zur Geltung.
Aus diesen Gründen wird als
Grenze für die Maximalvergrößerung nicht D [mm]* 0,43, sondern
![]() (7)
(7)
empfohlen. Für Refraktoren
findet man sogar D [mm] * 2,5.
Die zugehörige minimale
Brennweite des Okulars ist dann
![]() (8)
(8)
Dies liefert für ein System mit
1000mm Brennweite und 100mm Objektiv z.B. 5mm minimale Okularbrennweite.
Gesichtsfeld
Zu unterscheiden sind die
beiden Begriffe „scheinbares Gesichtsfeld (SG)“ und „tatsächliches Gesichtsfeld
(TG)“.
Das scheinbare Gesichtsfeld
ist eine Eigenschaft des Okulars, nämlich der Öffnungswinkel, den ich sehe,
wenn ich durch das Okular schaue. Je nach Bauart sind scheinbare Bildwinkel
zwischen ca. 30° (Okulare nach Huygens) und ca. 82° (Nagler) möglich.
Anschaulich gesprochen erweckt ein Huygens-Okular den Eindruck, als würde man
durch einen Tunnel blicken, während man beim Einblick in ein Nagler-Okular in
der ersten Kinoreihe zu sitzen scheint.
Das tatsächliche
Gesichtsfeld ist das Himmelsareal, angegeben in Grad, das man beim Blick durch
das Teleskop überschauen kann. Es setzt sich zusammen aus dem scheinbaren
Gesichtsfeld des Okulars und der mit dem Okular erzielten Vergrößerung. Der
Bezug ist
![]() (9)
(9)
Bei gleicher Vergrößerung
erzielt man also mit Weitwinkelokularen (ca. 70° SG) ein tatsächliches
Gesichtsfeld mit dem 2,3-fachen Durchmesser gegenüber einem orthoskopischen
Okular (30° SG), d.h. die betrachtete Himmelsfläche ist um den Faktor 5,4
größer! Bei großflächigen Objekten drängt sich daher die Verwendung von
Weitwinkelokularen geradezu auf, der Eindruck am Teleskop ist unvergleichlich
imponierender.
Übliche tatsächliche
Gesichtsfelder reichen von ca. 3,2°, also mehr als dem 6-fachen Monddurchmesser
(31mm Nagler an einem Teleskop mit 800mm Brennweite), bis herunter zu einigen
Bogenminuten.
Hinweis für fortgeschrittene Leser:
Die Formel (9) ist zwar weit verbreitet und wird gerne benutzt (auch von
uns), streng genommen ist sie aber nicht richtig. Vernachlässigt wird bei
dieser Formel, dass Okulare nicht verzeichnungsfrei sind (sein können), wodurch
die Vergrößerung über das gesamte Gesichtsfeld keine Konstante ist. Bei
kissenförmiger Verzeichnung steigt die Vergrößerung zum Rand hin. Da wir bei
unserer Bestimmung des scheinbaren Gesichtsfeldes über diese Formel rechnen,
sind unsere so ermittelten scheinbaren Gesichtsfelder je nach Stärke der Verzeichnung
eher etwas kleiner (ca. 0° bis 3°) als die der Definition entsprechenden
scheinbaren Gesichtsfelder. Der Vorteil ist jedoch, dass die Formel (9), wenn
unsere ermittelten scheinbaren Gesichtsfelder benutzt werden, das richtige
Ergebnis für das tatsächliche Gesichtsfeld liefert. Der Nachteil ist, dass
hierdurch inhärente Unterschiede in den scheinbaren Gesichtsfeldern, wie sie
von den Herstellern angegeben werden, und unseren bestehen.
Das maximale scheinbare
Gesichtsfeld ist physikalisch begrenzt und ergibt sich aus der Okularbrennweite
und dem Durchmesser der Feldlinse bzw. der Feldblende zu
![]() (10)
(10)
Zur
Beachtung: Rechnet man mit dem Taschenrechner in der Einstellung „DEG“, dann
entfällt der Faktor 180/π (arctan im Bogenmaß!). Ist die Einstellung auf
„RAD“ oder rechnet man mit Excel, dann die Formel bitte wie angegeben benutzen.
Da die Größe der Feldlinse
durch den Okulardurchmesser eine natürliche Grenze hat, haben Okulare mit 24,5,
31,8mm und 50,8mm Durchmesser entsprechend ihrer Brennweite ein maximales
scheinbares Gesichtsfeld (s. folgende Tabelle). Das angegebene Gesichtsfeld ist
theoretisch, da die Einsteckhülse eine gewisse Wandstärke haben muss, sind die
tatsächlich erreichbaren Gesichtsfelder einige wenige Grad kleiner.
|
Einsteckdurchmesser |
Okularbrennweite (mm) |
maximales scheinbares
Gesichtsfeld (°) |
|
24,5mm |
15 |
78,5 |
|
|
20 |
63,0 |
|
|
25 |
52,2 |
|
|
30 |
44,4 |
|
|
40 |
34,1 |
|
31,8mm (1 ¼“) |
15 |
93,3 |
|
|
20 |
77,0 |
|
|
25 |
64,9 |
|
|
30 |
55,8 |
|
|
40 |
43,4 |
|
50,8mm (2“) |
25 |
90,9 |
|
|
30 |
80,5 |
|
|
40 |
64,8 |
|
|
50 |
53,9 |
|
|
80 |
35,2 |
Tabelle 1:
Maximal mögliche scheinbare Gesichtsfelder für Okulare mit verschiedenen
Einsteckdurchmessern und Brennweiten.
Größere scheinbare
Gesichtsfelder sind verzeichnungsfrei nicht erreichbar! An dieser Tabelle sieht
man auch, warum und wo 2“-Okulare ihre Berechtigung haben: Bei langen
Brennweiten, wenn das gewünschte
scheinbare Gesichtsfeld mit einem Okular kleineren Einsteckdurchmessers
nicht mehr zu erreichen ist. Bei einer Brennweite von z.B. 15mm sehe ich
dagegen selbst mit einem Ultraweitwinkel exakt dasselbe mit 2“ wie auch mit 1
¼“-Okularen.